
The bin packing problem is a combinatorial optimization problem in which items of different sizes must be packed into a number of containers with a fixed capacity in such a way that the number of containers used is minimized. This website of the lamarr-institute provides a nice and clear explanation of the bin-packing problem and covers the various types of construction heuristics.
As with other problems in operations research, a distinction is made here between the variant where all items to be packed are known in advance – referred to as the offline variant – and the variant where only the next item is known, requiring decisions on which container to place the item with limited information – referred to as the online variant.
In this post, we will develop a construction heuristic for the offline variant of the bin packing problem.
Common methods that come to mind when trying to solve the problem manually are referred to in the literature as first-fit decreasing or best-fit decreasing. We first sort the items in descending order by volume (or weight or any another property of interest). In the first-fit method, we sequentially check each used container and place the item in the first container where there is enough space.
In the best-fit approach, we place the item in the container with the minimal remaining space after the item has been inserted. In this poast, we will develop a heuristic for this variant.
Best-Fit Construction Heuristic
The best fit construction heuristic can be described as follows:
- Sort all items in descending order by volume.
- Sequentially process each item and place it in the container where, after placement, the remaining capacity is minimized.
- If no such container can be found, start a new container.
Problem Instances
To provide something to work with, here are a few generated problem instances. I have created a simple data format to describe test instances for the bin-packing problem and a basic problem instance generator that produces reasonably useful test cases.
| Instance File Name | Container Size | Number of Items |
| BIN_PACK_1D_C10_O5 | 10 | 5 |
| BIN_PACK_1D_C10_O20 | 10 | 20 |
| BIN_PACK_1D_C25_O60 | 25 | 60 |
I’ve designed the file format for describing bin packing problem instances similar to the TSP format, aiming to keep it human-readable and easy to process, both for reading and generating data. The BIN_PACK_1D_C10_O5.bpk instance looks as follows:
NAME: BIN_PACK_1D_C10_O5
TYPE: 1D-BIN PACKING INSTANCE
COMMENT: Place 5 objects in 1-dimensional bins with capacity 10
CONTAINER_CAP: 10
OBJ_ID_DIM
1 1.1
2 4.3
3 3.9
4 1.6
5 2.7
EOFAs always, we start by creating a few very simple problem instances to validate our heuristic implementation, as the expected solution can be easily determined.
Implementation of the Construction Heuristic
We are now ready to translate the heuristic into program code. Based on the description above, this can be done directly with the help of ChatGPT.
The basic pattern of the heuristic can easily be sketched. One consideration remains regarding the storage of items. Using a dictionary to store item-ids along with their volumes is preferable to using a list. Our heuristic could be coded as follows:
def binpack_greedy(items, container_cap):
"""
construction of a best-fit heuristic to generate a fairly good offline 1d-binpacking solution.
:param items: the dict of items to be packed; key is index, value is dimension
:param container_cap: the capacity of each (standard) container
:return: a dictionary containing lists of object_ids to be packed in each container, the number of containers needed
"""
# Sort the jobs by duration in descending order
# sorted_items = sorted(range(len(items)), key=lambda x: items[x], reverse=True)
sorted_items = dict(sorted(items.items(), key=lambda item: item[1], reverse=True))
assert container_cap > 0, "expected container_cap to be > 0!"
# Initialize a list to keep track of all containers required
resulting_containers = [[]]
# loop through all objects
for item_id, item in sorted_items.items():
if item > container_cap:
# instance not feasible
resulting_containers = None
break;
# determine best container id
best_cont_index = find_best_container(resulting_containers, container_cap, items, item)
# if no best container exists, start a new one
if best_cont_index == None:
resulting_containers.append([item_id])
else:
resulting_containers[best_cont_index].append(item_id)
return resulting_containers, len(resulting_containers)We have elegantly outsourced the functionality for identifying the suitable container into the function find_best_container(). Since we implement the best-fit variant of the offline bin packing problem construction heuristic, we check every container and consider the one with the lowest left over capacity to be the best one. We can quickly find a good implementation for this with the help of ChatGPT:
def find_best_container(resulting_containers, container_cap, items, item):
"""
loops through all existing containers in the resulting_containers (lists in list) and returns the index
of the container with the minimal leftover capacity after adding item item.
:param resulting_containers: the list containing lists of item_ids of the packed containers
:param container_cap: container capacity
:param items: the dict of all items with their volume
:param item: the item to be packed
:return: the index of the best container or None
"""
container_leftover_capacity = []
for container in resulting_containers:
container_volume = [items.get(item_id) for item_id in container]
container_leftover_capacity.append(container_cap - sum(container_volume) - item)
best_leftover = math.inf
best_container_id = None
# find container-id with minimal leftover capacity
for container_id, leftover_cap in enumerate(container_leftover_capacity):
if leftover_cap >= 0 and leftover_cap < best_leftover:
best_leftover = leftover_cap
best_container_id = container_id
return best_container_idWhen formulating the prompt for ChatGPT, it’s important to specify the exact data types we need. The used containers are stored as a list of lists, where we keep the item IDs of the items placed in each container. For this function I did not manage ChatGPT to produce the source I wanted. The Issue was, that when calculating the remaining capacity of each container, we need to first look up the volume of each packed item in the items dictionary.
It’s important to note that a lot of repetitive calculations are being performed here. A more efficient approach would be to keep track of the volume of each container and only update it when adding an item. If speed is a priority, this optimization would be necessary. However, since construction heuristics are typically fast enough without additional optimization, we can initially omit this step and address it only if performance becomes an issue. As soon as we’re developing improvement heuristics (such as local search), such delta calculations will become essential.
The complete source code can be found here.
Validation of the Implementation
As the final step, we should review the implementation to ensure it performs as expected. Visualizing the solutions can help, as graphical representation often makes it easier and faster to identify errors than simply examining the data.
Thanks to ChatGPT, we can now develop a method to visualize solutions in just a few minutes. For example, with the following prompt, I created a plot method that visualizes our bin-packing solutions:
Write a Python function plot_binpack_problem(items, container_cap, resulting_containers). items is a dictionary with item IDs as keys and volumes as values. container_cap is the capacity of the containers used, and resulting_containers is a list of lists, where each list corresponds to a container and contains the item IDs that have been assigned to that container. The function should plot the individual containers and display the contents (volumes) on the y-axis in a proportional manner.dfdf
With the resulting plot_binpack_problem() function, we can visualize the solutions and check them for plausibility. You can find the function in the complete source code provided here. Below are the graphics for the three test instances.
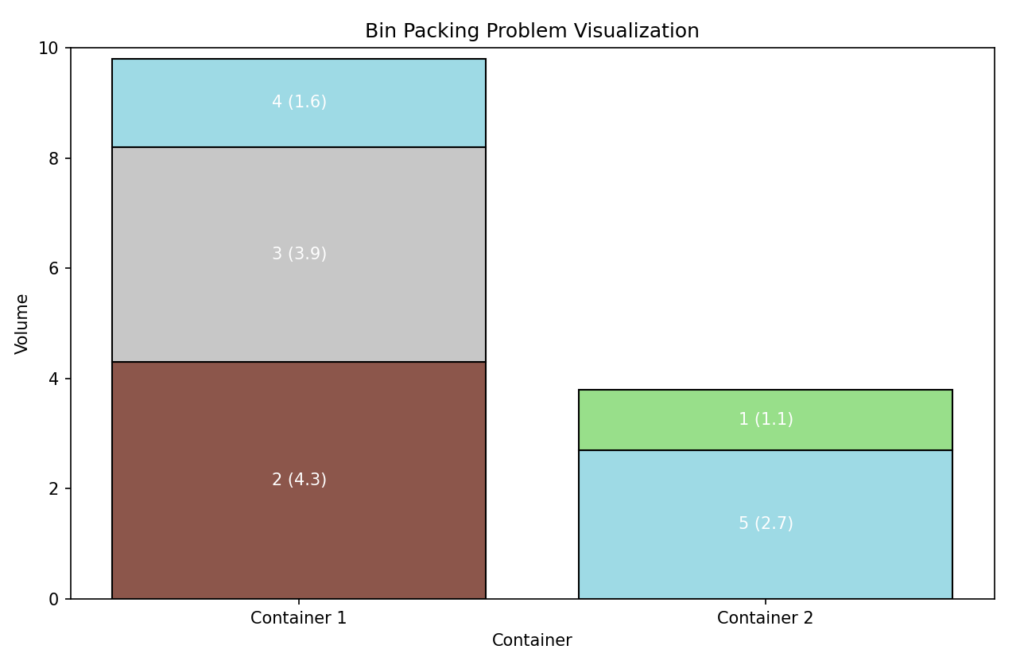

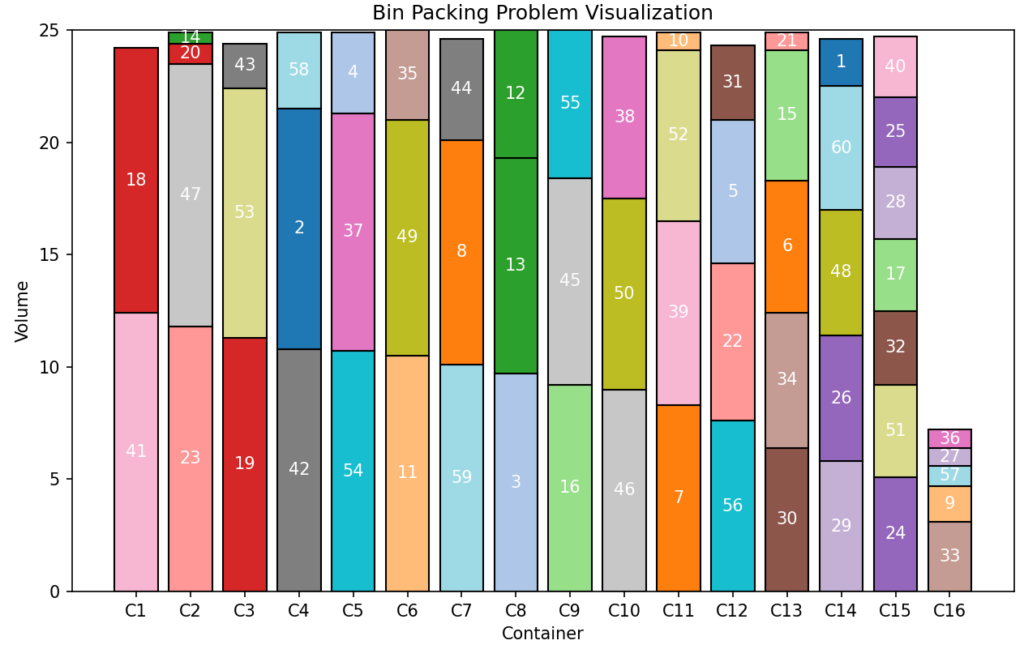
The solution, particularly for the first problem instance, is easy to verify and seems plausible. Adherence to the container capacity can also be easily checked thanks to the indication of item IDs as well as the item volumes.