
In this post, we develop a construction heuristic to generate a first solution to the Traveling Salesman Problem (TSP). This is a simple heuristic which starts from an arbitrarily chosen location and then visits the nearest neighbor until all nodes have been visited. Finally, the tour is completed by returning to the starting node.
Problem Instances
To begin, we need some compelling problem instances. We select a few from the well-known TSPLIB, provided by the University of Heidelberg.
- berlin52: 52 locations in Berlin (Groetschel)
- u1817: Drilling problem (Reinelt), Dimension 1’827
- u2319: Drilling problem (Reinelt),Dimension 2’319
The TSP instances we take care of come in the form of the simple tsp-file format, listing the coordinates of all nodes (vertices) to be visited in the euclidean space:
NAME: berlin52
TYPE: TSP
COMMENT: 52 locations in Berlin (Groetschel)
DIMENSION: 52
EDGE_WEIGHT_TYPE: EUC_2D
NODE_COORD_SECTION
1 565.0 575.0
2 25.0 185.0
3 345.0 750.0
4 945.0 685.0
...
EOFThe following function helps us to read the TSP instances for further processing:
def read_tsp_file(file_path):
"""
read TSPlib input file and return a nodes-dictionary
:param file_path:
:return: dict containing nodes with tupels representing x, y coordinates
"""
nodes = {}
with open(file_path, 'r') as file:
lines = file.readlines()
node_section = False
for line in lines:
line = line.strip()
if line.startswith("NODE_COORD_SECTION"):
node_section = True
continue
if line.startswith("EOF"):
break
if node_section:
parts = line.split()
if len(parts) == 3:
node_id, x, y = parts
nodes[int(node_id)] = (float(x), float(y))
return nodesThe function returns a list of nodes to be combined in a TSP tour.
The Nearest Neigbhor Construction Heuristic
As mentioned, the nearest neighbor heuristic starts from an arbitrarily chosen location and then visits the nearest unvisited neighbor location until all locations have been visited. The following graph shows, how this heuristic behaves.
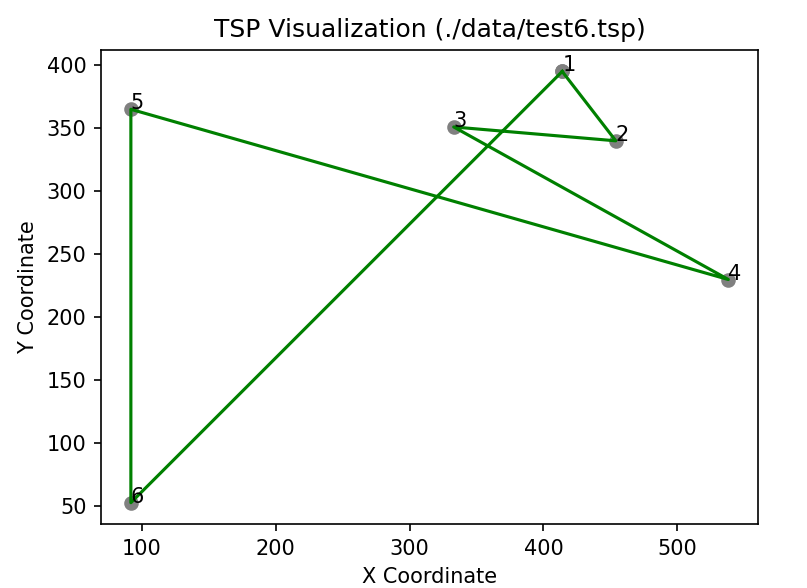
Of course this is not a very good result, if our objective was to find minimal distance tours. No let’s check, what result we get, when we would trigger the NN-heuristic starting from node (6):
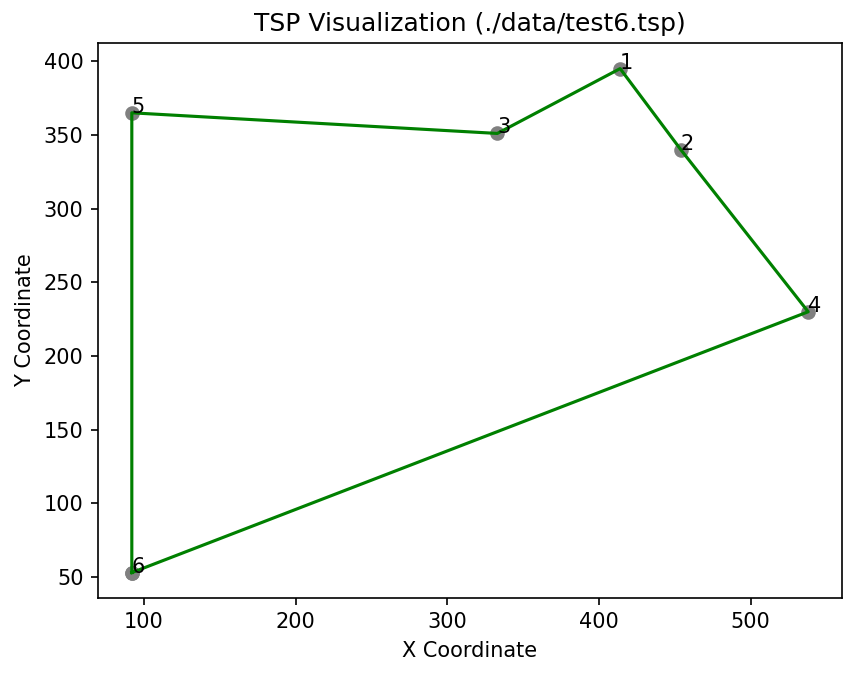
This experiment highlights both the strengths and weaknesses that often come with using heuristic approaches. Heuristics can find good or bad solutions depending on how they’re being initialized. When playing with heuristics, we find that the quality of their solutions vaiers across different problem instances. It is always possible to create problem instances where a specific heuristic performs poorly.
For the NN-heuristic the quality of the tours found depends on the selected starting location. To address this, one could consider improving the NN heuristic by calculating all possible variants and returning the best one. This way, we could have found the optimal solution using just the construction heuristic, at least in the example above.
Even though some heuristics can find optimal solutions for certain types of problems, we usually can’t expect construction heuristics to do so. In future posts, we’ll explore improvement heuristics (local search heuristics) that help us further refine and improve existing solutions.
Now let’s formalize, how the NN-heuristic works. In simple words, the heuristic can be formulated as follows:
- start the tour at a given location
- always move to the next unvisited node until all locations have been visited
- return to the starting location
For experienced programmers, this description is sufficient to implement the heuristic. The description is fully adequate and precise enough to define the behavior of the heuristic. However, for beginners, it might be helpful to break down the approach in a bit more technical detail. A description could then look like this, for example:
I) Initialization
- Initialize the list L with all nodes to be visited.
- Initialize an empty list for the TSP tour T = [].
- Randomly select a specific node as the starting node, remove it from L, and add it to T.
II) While L is not empty
- Find the node among all unvisited nodes in L that is closest to the last visited node. Remove this node from L and add it to T.
III) Complete the tour T by returning to the starting node
The translation into python is straight forward and can be gathered directly using ChatGPT or some other AI Tools based on the heuristic pseudocode:
def nearest_neighbor_tsp(start_node, nodes):
unvisited = set(nodes.keys())
tour = [start_node]
unvisited.remove(start_node)
total_distance = 0.0
current_node = start_node
while unvisited:
next_node = min(unvisited, key=lambda node: calculate_distance(nodes[current_node], nodes[node]))
distance = calculate_distance(nodes[current_node], nodes[next_node])
total_distance += distance
tour.append(next_node)
unvisited.remove(next_node)
current_node = next_node
# Add distance back to the start to complete the tour
total_distance += calculate_distance(nodes[current_node], nodes[start_node])
return tour, total_distance
Since in our simple TSP instacnes we only allow euclidic distances, we can just use the pythagoras to calculate the distances from the coordinates:
def calculate_distance(coord1, coord2):
return math.sqrt((coord1[0] - coord2[0]) ** 2 + (coord1[1] - coord2[1]) ** 2)For small instances, this is ok, while for larger ones we would want to precalculate a distance matrix or use memoization to cache return values to function calls.
The Complete Source
That’s it! We’re done. Now we finish the code implementing a main to solve all instances provided together with the index of a deliberately chosen starting location for the TSP tours:
# Samplescript UKO01.PROG Nearest Neighbor K-Heuristik
import math
def calculate_distance(coord1, coord2):
return math.sqrt((coord1[0] - coord2[0]) ** 2 + (coord1[1] - coord2[1]) ** 2)
def nearest_neighbor_tsp(start_node, nodes):
unvisited = set(nodes.keys())
tour = [start_node]
unvisited.remove(start_node)
total_distance = 0.0
current_node = start_node
while unvisited:
next_node = min(unvisited, key=lambda node: calculate_distance(nodes[current_node], nodes[node]))
distance = calculate_distance(nodes[current_node], nodes[next_node])
total_distance += distance
tour.append(next_node)
unvisited.remove(next_node)
current_node = next_node
# Add distance back to the start to complete the tour
total_distance += calculate_distance(nodes[current_node], nodes[start_node])
return tour, total_distance
def read_tsp_file(file_path):
"""
read TSPlib input file and return a nodes-dictionary
:param file_path:
:return: dict containing nodes with tupels representing x, y coordinates
"""
nodes = {}
with open(file_path, 'r') as file:
lines = file.readlines()
node_section = False
for line in lines:
line = line.strip()
if line.startswith("NODE_COORD_SECTION"):
node_section = True
continue
if line.startswith("EOF"):
break
if node_section:
parts = line.split()
if len(parts) == 3:
node_id, x, y = parts
nodes[int(node_id)] = (float(x), float(y))
return nodes
def main():
file_paths = ['./data/berlin52.tsp', './data/u1817.tsp', './data/u2319.tsp']
start_nodes = [1, 257, 2319]
for id, file in enumerate(file_paths):
nodes = read_tsp_file(file)
tour, dist = nearest_neighbor_tsp(start_nodes[id], nodes)
print(f"*** File {file}, with start node {id}:")
print(f"Tour: {tour[:5]}")
print(f"Dist: {round(dist)}")
if __name__ == "__main__"
main()
Validation of the Implementation
The whole script with unittests is also available here. We use pytest here to develop two tests to validate, whether our implementation works correctly.
To validate the functionality of the code, it usually makes sense to create simple test instances the solution is easy to predict for. For example, you can create a tour through the four corners of a square or, more generally, through the corners of a polygon to check if the result matches the expected outcome. Here are the corresponding test instances, test4.tsp and test8.tsp.
Since it’s easier to validate the results visually, we’re developing a feature that displays the routes in the Euclidean plane. Ask ChatGPT to help you, so it’s a matter of seconds. You get best results when you provide the input arguments and let ChatGPT know, what return expect the method to do.
def plot_tsp_solution(nodes, solution, title):
# Extract coordinates
x_coords = [nodes[node][0] for node in solution]
y_coords = [nodes[node][1] for node in solution]
# Add the start point to the end to complete the tour
x_coords.append(nodes[solution[0]][0])
y_coords.append(nodes[solution[0]][1])
# Plot the nodes
plt.scatter(x_coords, y_coords, c='gray')
# Plot the path
plt.plot(x_coords, y_coords, c='green')
# Annotate the nodes
if len(nodes) < 200:
for idx, node in enumerate(solution):
plt.annotate(str(node), (x_coords[idx], y_coords[idx]))
plt.xlabel('X Coordinate')
plt.ylabel('Y Coordinate')
plt.title('TSP Visualization (' + title + ')')
plt.show()The results for the test instances test4.tsp and test8.tsp turn out as follows:
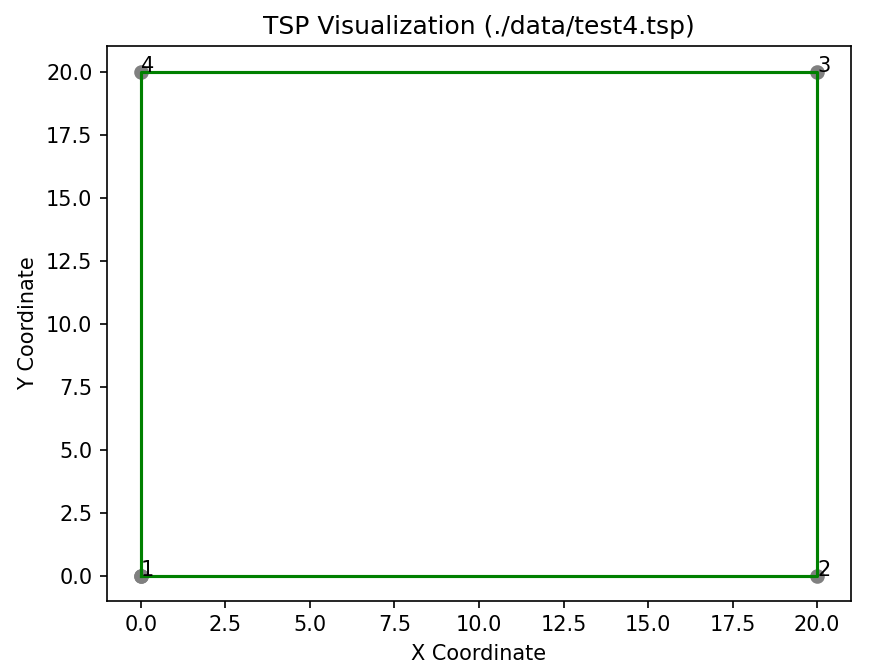
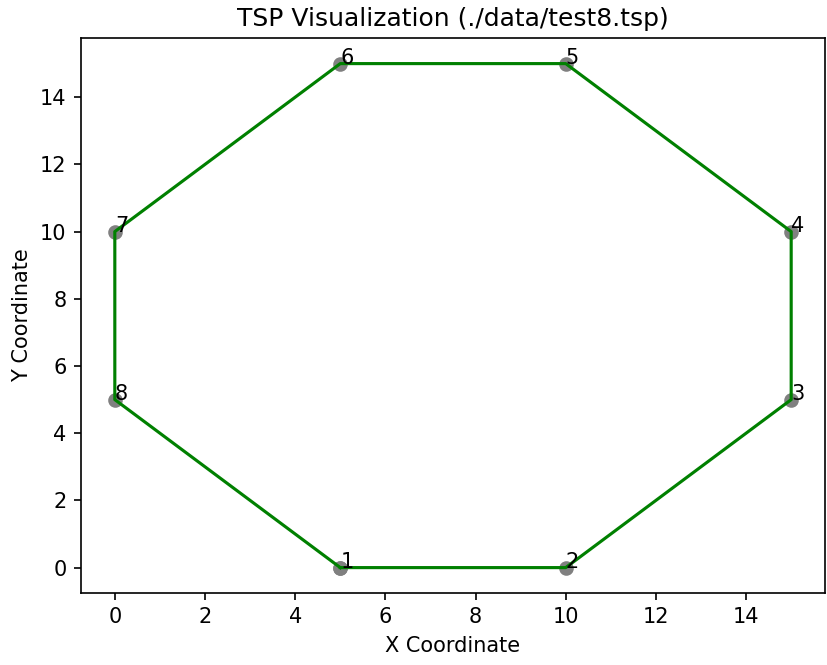
Refer to the post How to Improve TSP-Tours Applying the 2-opt Neighborhood for an understanding of how simple initial solutions can be improved through the application of improvement heuristics and local search methods.