For years, my Android unlock pattern was my fortress — a carefully chosen sequence of swipes that I thought only I could remember. Unfortunately, I underestimated two things: (1) the persistence of children, and (2) their uncanny ability to casually “observe” without being noticed.
One day, I realized my long-guarded pattern had been compromised. My kids, apparently, had been running a covert surveillance operation worthy of a spy novel. The breach left me with only one option: design a new pattern that would be far more difficult to guess — even if observed a couple of times.
Being both mildly paranoid and a fan of Operations Research, I decided to solve this in python as a nice little graph problem:
- The pattern must be complex (non-obvious, no straight-lines, and making full use of the grid).
- It should avoid common shapes (no easy diagonals, squares, or simple zig-zags).
- It should be extra-hard to remember (so that I don’t need to learn a new pattern too soon)
Enter Python. Using some graph theory tools, I modeled the Android pattern grid as a fully connected set of points with constraints. Then, I applied a simple algorithm to generate candidate patterns. For every node I provided the allowed neighbors. The result? A beautifully tangled path that looks like it belongs in a combinatorics textbook rather than on a smartphone screen.
Here’s a sample visualization:
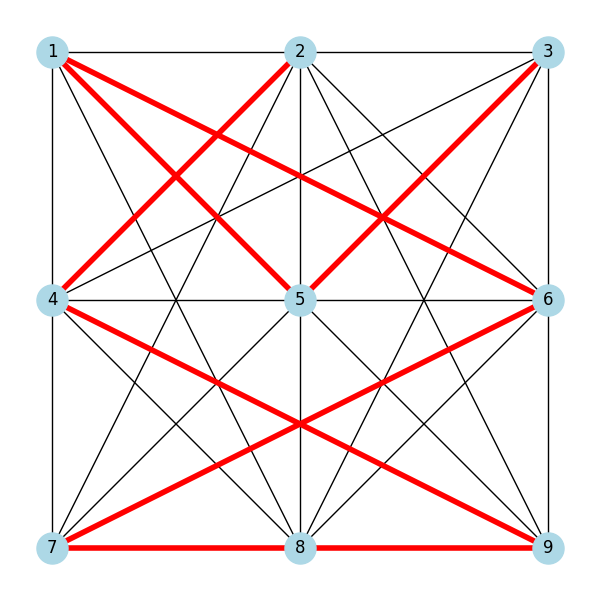
With this new approach, my phone is now protected by a pattern that would take my kids either a small miracle or a semester-long graph theory course to crack.
At the end of this post, you’ll find the Python code that implements the pattern generator and scoring system. I’d love to hear thoughts on how the algorithm could be improved — perhaps integrating more advanced optimization methods like simulated annealing or genetic algorithms.
And now for the fun part — the code!
After all this talk about graphs, complexity, and the perils of curious children, it’s time to get practical. Below is the Python script I developed to generate and evaluate complex unlock patterns on a 3×3 grid (modeled as the complete graph K9K_9K9). This code takes care of creating the grid, connecting every node to every other node, and then selecting paths that maximize pattern complexity.
import random
import networkx as nx
import matplotlib.pyplot as plt
from itertools import permutations
# Generator für zufällige Android-Sperrmuster in einem 3x3-Gitter
# Adjazenzliste
adj_list = {
1: [2, 6, 5, 8, 6],
2: [1, 4, 7, 5, 9, 6, 3],
3: [2, 4, 5, 8, 6],
4: [1, 2, 3, 5, 9, 8, 7],
5: [1, 2, 3, 6, 9, 8, 7, 4],
6: [3, 2, 1, 5, 7, 8, 9],
7: [4, 2, 5, 6, 8],
8: [7, 4, 1, 5, 3, 6, 9],
9: [6, 2, 5, 4, 8]
}
# Koordinaten
positions = {
1: (0, 2), 2: (1, 2), 3: (2, 2),
4: (0, 1), 5: (1, 1), 6: (2, 1),
7: (0, 0), 8: (1, 0), 9: (2, 0)
}
# Graph erstellen
G = nx.Graph()
for node, neighbors in adj_list.items():
for neighbor in neighbors:
G.add_edge(node, neighbor)
# Alle Permutationen der Knoten (1 bis 9), die gültige Pfade sind
def is_valid_path(path):
return all(path[i+1] in adj_list[path[i]] for i in range(len(path) - 1))
nodes = list(range(1, 10))
valid_paths = [p for p in permutations(nodes) if is_valid_path(p)]
# Visualisierung der ersten paar gültigen Pfade
def draw_path(path, index):
plt.figure(figsize=(6, 6))
nx.draw(G, pos=positions, with_labels=True, node_color='lightblue', node_size=500)
edges_in_path = [(path[i], path[i+1]) for i in range(len(path)-1)]
nx.draw_networkx_edges(G, pos=positions, edgelist=edges_in_path, edge_color='red', width=4)
plt.title(f"Gültiger Pfad #{index+1}")
plt.show()
while True:
i = random.randint(0, len(valid_paths) - 1)
print(valid_paths[i], f"is a valid path with i={i}.")
draw_path(valid_paths[i], i)